Trace refers to the line of intersection between a plane and another surface, while a plane is a flat, two-dimensional surface extending infinitely in all directions. When visualizing geometric problems, understanding how your plane interacts with other shapes through traces helps in accurately determining spatial relationships.
Table of Comparison
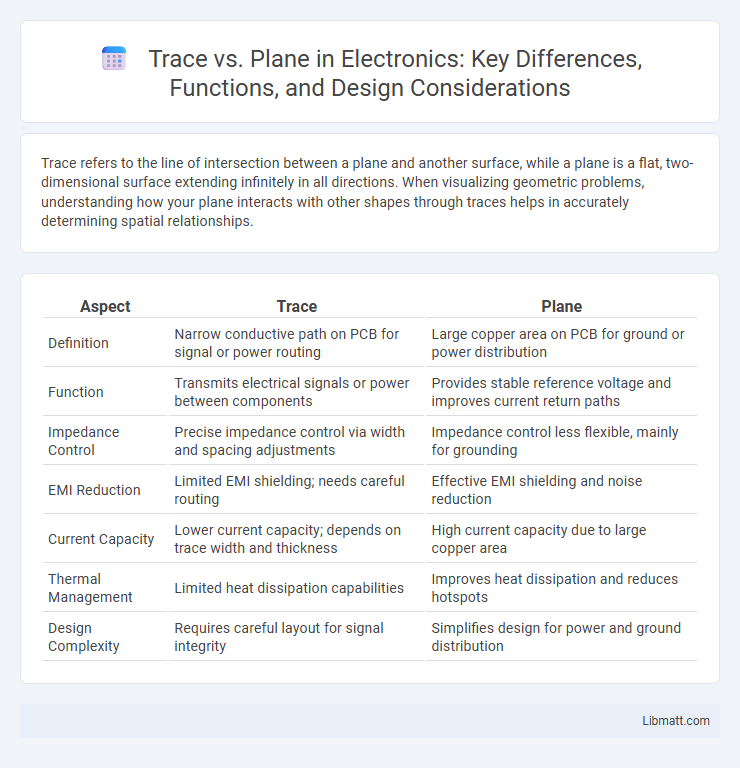
| Aspect | Trace | Plane |
|---|---|---|
| Definition | Narrow conductive path on PCB for signal or power routing | Large copper area on PCB for ground or power distribution |
| Function | Transmits electrical signals or power between components | Provides stable reference voltage and improves current return paths |
| Impedance Control | Precise impedance control via width and spacing adjustments | Impedance control less flexible, mainly for grounding |
| EMI Reduction | Limited EMI shielding; needs careful routing | Effective EMI shielding and noise reduction |
| Current Capacity | Lower current capacity; depends on trace width and thickness | High current capacity due to large copper area |
| Thermal Management | Limited heat dissipation capabilities | Improves heat dissipation and reduces hotspots |
| Design Complexity | Requires careful layout for signal integrity | Simplifies design for power and ground distribution |
Introduction to Trace and Plane
Trace and Plane are fundamental concepts in geometry, where a trace refers to the intersection line between a plane and a coordinate axis or another plane. A plane is a flat, two-dimensional surface extending infinitely in all directions, defined by three non-collinear points or a point and a normal vector. Understanding the relationship between traces and planes enables you to solve complex spatial problems and analyze geometric structures effectively.
Defining Trace: Meaning and Usage
Trace refers to the intersection line or curve formed when a plane cuts through a solid object or geometric shape, representing the exact location where the plane meets the object. In geometry and computer graphics, understanding the trace is essential for visualizing projections, mapping surfaces, and analyzing spatial relationships. Your ability to define and utilize the trace enhances accuracy in design, modeling, and mathematical problem-solving.
Understanding Plane: Concepts and Applications
Plane refers to a flat, two-dimensional surface extending infinitely in length and width, foundational in geometry and computer graphics. Understanding plane concepts enables precise modeling, as planes serve as reference surfaces for drawing, tracing, and constructing 3D environments. Your ability to work with planes enhances accuracy in design, virtual simulations, and spatial analysis across various applications.
Key Differences Between Trace and Plane
Trace and plane differ primarily in dimensions; a trace is a one-dimensional line, while a plane is a two-dimensional flat surface extending infinitely. Traces represent the intersection of surfaces or the trajectory of points, whereas planes are defined by at least three non-collinear points or a normal vector and a point. In mathematics and computer graphics, traces are used for visualizing cross-sections, and planes serve as fundamental constructs for modeling and spatial analysis.
The Role of Traces in Geometry
Traces in geometry represent the intersection lines formed when a plane cuts through a three-dimensional object, providing crucial insights into its spatial structure. These intersection lines, or traces, help determine properties such as angles, distances, and shapes within the object's coordinate system. Understanding traces enables precise visualization and analysis of geometric configurations in fields like computer graphics, engineering, and architecture.
Applications of Planes in Mathematics
Planes serve as fundamental elements in geometry, enabling the study of two-dimensional surfaces within three-dimensional space. They are essential in vector calculus for defining gradients, flux, and surface integrals. In linear algebra, planes represent solutions to linear equations and provide a setting for analyzing vector spaces and transformations.
Trace vs Plane: Visual Representation
Trace represents the exact path or trajectory of an object or point in space, often visualized as a line or curve highlighting movement over time. Plane refers to a two-dimensional flat surface extending infinitely in all directions, usually depicted as a grid or shaded area to emphasize spatial relationships. Visualizing trace versus plane helps distinguish between dynamic motion paths and static spatial frameworks in fields like geometry, physics, and computer graphics.
Practical Examples: Trace and Plane in Real Life
Trace and plane concepts are essential in fields like architecture, where blueprints (planes) represent structures in two dimensions while laser scans (traces) capture exact three-dimensional details. In engineering, CNC machining relies on plane definitions to guide tool paths, whereas traces help verify the precision of cuts against the design. Understanding how trace data maps onto planes can enhance your accuracy in manufacturing and design projects.
Common Mistakes When Distinguishing Trace and Plane
Common mistakes when distinguishing trace and plane often stem from confusing the trace, a line representing the intersection of a plane with a coordinate axis or reference plane, with the plane itself. Many misunderstand that the trace is not the entire geometric surface but merely a projection or intersection line used to define the plane's orientation in space. Failing to recognize that multiple traces correspond to a single plane can lead to errors in visualizing spatial relationships and solving geometric problems.
Summary and Conclusion: Choosing Trace or Plane
Choosing between Trace and Plane largely depends on the specific application and data visualization needs. Trace is ideal for detailed, continuous data representation, offering precise insights into trends and patterns over time. Plane, on the other hand, excels in spatial analysis and area-based visualizations, providing clearer context for geographic or planar data distributions.
Trace vs Plane Infographic
 libmatt.com
libmatt.com