PID control offers simplicity and ease of implementation, making it effective for systems with well-understood dynamics and requiring straightforward, real-time adjustments. LQR control provides optimal state feedback by minimizing a quadratic cost function, enhancing performance in complex, multi-variable systems where precision and stability are critical to your application.
Table of Comparison
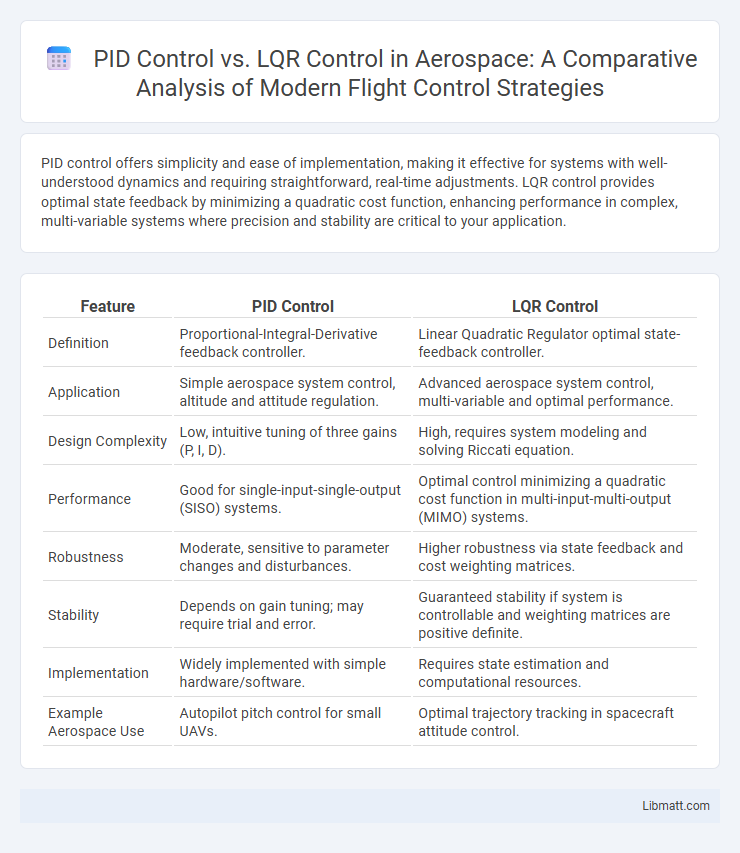
| Feature | PID Control | LQR Control |
|---|---|---|
| Definition | Proportional-Integral-Derivative feedback controller. | Linear Quadratic Regulator optimal state-feedback controller. |
| Application | Simple aerospace system control, altitude and attitude regulation. | Advanced aerospace system control, multi-variable and optimal performance. |
| Design Complexity | Low, intuitive tuning of three gains (P, I, D). | High, requires system modeling and solving Riccati equation. |
| Performance | Good for single-input-single-output (SISO) systems. | Optimal control minimizing a quadratic cost function in multi-input-multi-output (MIMO) systems. |
| Robustness | Moderate, sensitive to parameter changes and disturbances. | Higher robustness via state feedback and cost weighting matrices. |
| Stability | Depends on gain tuning; may require trial and error. | Guaranteed stability if system is controllable and weighting matrices are positive definite. |
| Implementation | Widely implemented with simple hardware/software. | Requires state estimation and computational resources. |
| Example Aerospace Use | Autopilot pitch control for small UAVs. | Optimal trajectory tracking in spacecraft attitude control. |
Introduction to PID and LQR Control
PID control uses proportional, integral, and derivative terms to maintain system stability by correcting errors based on past, present, and predicted future values. LQR (Linear Quadratic Regulator) control optimizes system performance by minimizing a cost function that balances control effort and error magnitude through state feedback. Your choice between PID and LQR depends on the complexity of the system and the desired level of optimality in control.
Fundamental Concepts of PID Control
PID control relies on proportional, integral, and derivative terms to continuously correct system errors, making it ideal for straightforward, real-time adjustments. The proportional term addresses the current error, the integral term eliminates steady-state error by summing past errors, and the derivative term predicts future error trends to improve stability. You benefit from PID control's simplicity and ease of tuning in processes requiring reliable, linear feedback without complex state-space modeling.
Fundamental Concepts of LQR Control
LQR Control, based on optimal control theory, minimizes a cost function balancing state error and control effort, providing a systematic way to achieve desired system performance. Unlike PID Control, which relies on heuristic tuning of proportional, integral, and derivative gains, LQR uses state feedback and solves the Riccati equation for optimal gain calculation. You can leverage LQR Control for multivariable systems requiring precise regulation and robustness against disturbances.
Mathematical Foundations: PID vs LQR
PID control relies on proportional, integral, and derivative terms to minimize the error between a desired setpoint and the system output, based on time-domain error dynamics. LQR control formulates an optimal control problem by minimizing a cost function that balances state deviations and control effort, using the solution of the Riccati equation derived from system state-space models. While PID is grounded in classical control theory emphasizing error correction, LQR is rooted in modern optimal control theory leveraging system dynamics matrices and quadratic cost criteria.
Tuning and Parameter Optimization
PID control tuning involves adjusting proportional, integral, and derivative gains to balance responsiveness and stability, often using methods like Ziegler-Nichols or trial-and-error for parameter optimization. LQR control requires solving a Riccati equation to minimize a quadratic cost function, where weighting matrices Q and R are selected to prioritize state errors versus control effort, enabling systematic parameter optimization through linear algebra techniques. While PID tuning is heuristic and manual, LQR tuning is model-based and computational, allowing for more precise and optimal control performance in complex systems.
Performance Metrics: Stability and Robustness
PID control offers straightforward tuning and reliable stability for many linear systems but may struggle with robustness under significant model uncertainties or external disturbances. LQR control optimizes performance by minimizing a quadratic cost function, enhancing stability margins and robustness through state feedback that accounts for system dynamics comprehensively. Your choice depends on the complexity of the system and the required balance between simplicity and optimal robustness in performance metrics.
Applications in Real-World Systems
PID control is extensively used in industrial automation, temperature regulation, and motor speed control due to its simplicity and effectiveness in handling linear systems with steady-state errors. LQR control is favored in aerospace, robotics, and automotive systems where optimal performance and multi-variable system dynamics need to be managed simultaneously. Real-world deployments of LQR enable precise trajectory tracking and disturbance rejection, while PID remains the go-to for cost-effective, straightforward control tasks.
Advantages and Limitations Comparison
PID control offers simplicity and ease of implementation, making it ideal for systems with well-understood dynamics and requiring straightforward tuning. LQR control excels in handling multivariable systems with optimal performance by minimizing a quadratic cost function, but it demands accurate state-space models and higher computational resources. Your choice depends on system complexity, with PID favored for quick, robust control and LQR suited for precise, optimal regulation in advanced applications.
Implementation Challenges and Considerations
PID control offers a straightforward implementation with easily tunable parameters, making it suitable for systems with well-understood dynamics and minimal complexity. LQR control requires accurate state-space modeling and solution of Riccati equations, posing challenges in terms of computational resources and model accuracy. Your choice should reflect the system's complexity and available measurement capabilities, balancing simplicity against optimal performance.
Future Trends in Control Strategies
Emerging future trends in control strategies emphasize the integration of PID control and LQR control with machine learning and adaptive algorithms to enhance system robustness and real-time optimization. Advances in predictive analytics enable controllers to anticipate system disturbances and adjust parameters dynamically, improving performance in complex and nonlinear environments. Your control systems will benefit from hybrid approaches combining the simplicity of PID with the optimality and flexibility of LQR for smarter, more efficient automation.
PID Control vs LQR Control Infographic
 libmatt.com
libmatt.com