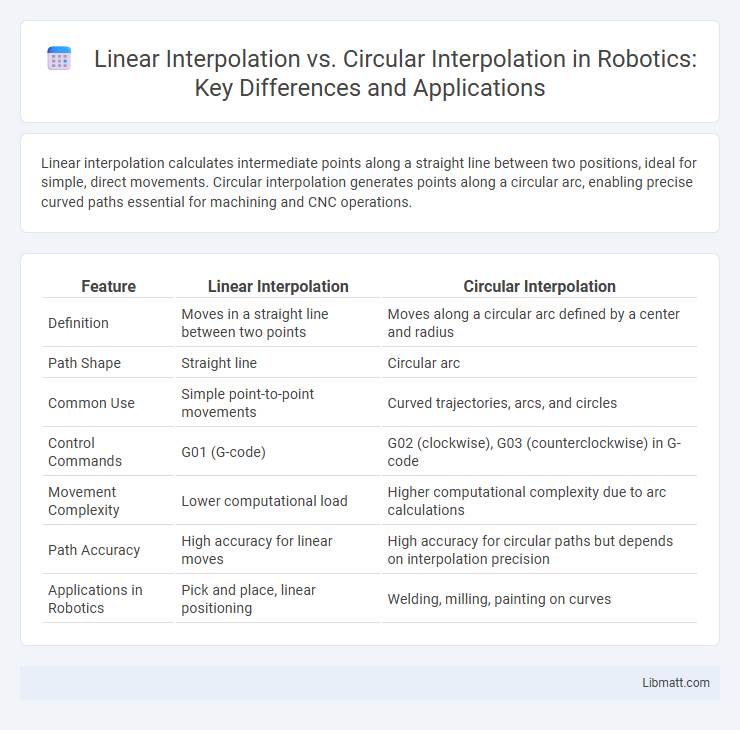
Linear interpolation calculates intermediate points along a straight line between two positions, ideal for simple, direct movements. Circular interpolation generates points along a circular arc, enabling precise curved paths essential for machining and CNC operations.
Table of Comparison
| Feature | Linear Interpolation | Circular Interpolation |
|---|---|---|
| Definition | Moves in a straight line between two points | Moves along a circular arc defined by a center and radius |
| Path Shape | Straight line | Circular arc |
| Common Use | Simple point-to-point movements | Curved trajectories, arcs, and circles |
| Control Commands | G01 (G-code) | G02 (clockwise), G03 (counterclockwise) in G-code |
| Movement Complexity | Lower computational load | Higher computational complexity due to arc calculations |
| Path Accuracy | High accuracy for linear moves | High accuracy for circular paths but depends on interpolation precision |
| Applications in Robotics | Pick and place, linear positioning | Welding, milling, painting on curves |
Introduction to Interpolation Methods
Linear interpolation connects two points using a straight line, providing a simple and efficient method for estimating values within the interval. Circular interpolation, also known as arc interpolation, calculates points along a circular path between two points defined by a center and radius, commonly used in CNC machining for curved tool paths. Both methods are fundamental in computer graphics, robotics, and manufacturing for smooth transitions and accurate positioning.
Defining Linear Interpolation
Linear interpolation calculates intermediate points by connecting two known data points with a straight line, providing a simple method for estimating values within the range. This technique assumes a constant rate of change between the points, making it ideal for applications that require uniform transitions, such as CNC machining or computer graphics. Unlike circular interpolation that generates arcs, linear interpolation strictly follows linear trajectories, ensuring direct and predictable motion paths.
Understanding Circular Interpolation
Circular interpolation defines a curved path between two points using a constant radius, enabling machines to accurately follow arcs or circles in CNC machining and robotics. Unlike linear interpolation, which moves tool heads or objects in straight lines, circular interpolation calculates intermediate positions along the circumference of a circle, ensuring smooth and precise curved toolpaths. Understanding circular interpolation helps optimize your machining processes for complex shapes, improving surface finish and dimensional accuracy.
Key Differences Between Linear and Circular Interpolation
Linear interpolation calculates intermediate points by connecting two data points with a straight line, ensuring uniform transitions along the X and Y axes. Circular interpolation, on the other hand, generates points along a defined circular arc, requiring parameters such as radius and center coordinates for accurate path formation. Understanding these key differences helps you select the appropriate interpolation method based on the desired precision and geometric path in CNC machining or computer graphics applications.
Mathematical Principles and Formulas
Linear interpolation calculates intermediate values between two points by assuming a straight-line relationship, using the formula \( y = y_1 + \frac{(x - x_1)(y_2 - y_1)}{x_2 - x_1} \). Circular interpolation involves calculating points along a circular arc, employing parametric equations \( x = x_c + r \cos \theta \) and \( y = y_c + r \sin \theta \), where \( (x_c, y_c) \) is the circle center, \( r \) the radius, and \( \theta \) the angle parameter. Understanding these mathematical formulas allows you to accurately program CNC machines or graphics rendering systems for smooth and precise path generation.
Applications in CNC Machining
Linear interpolation in CNC machining is primarily used for creating straight tool paths, ideal for cutting simple shapes and precise edges in materials such as metal or plastic. Circular interpolation enables the machine to follow curved paths, essential for machining arcs, circles, and complex rounded features with high accuracy. Understanding when to use linear versus circular interpolation optimizes your CNC programming for efficient material removal and superior surface finishes.
Advantages of Linear Interpolation
Linear interpolation offers precise control and simplicity when connecting two points with a straight line, making it ideal for applications requiring exact linear paths such as CNC machining. Its computational efficiency enables faster processing compared to circular interpolation, which involves more complex calculations for arcs. The straightforward implementation and predictability of linear interpolation reduce error margins in toolpath generation and improve machining accuracy.
Benefits of Circular Interpolation
Circular interpolation offers precise control over arc movements, enabling smoother and more accurate machining of curved surfaces compared to linear interpolation, which only moves in straight lines. This method reduces tool wear and enhances surface finish quality by maintaining continuous motion along a defined radius. You benefit from improved efficiency and precision in tasks such as CNC milling, where complex curves are essential.
Common Challenges and Solutions
Linear interpolation often faces challenges like maintaining smooth transitions and handling abrupt changes in slope, which can be addressed by employing higher-order interpolation methods or adaptive step sizing to improve accuracy. Circular interpolation frequently encounters issues with angle discontinuities and ensuring consistent rotational direction, solvable by implementing angle normalization techniques and quaternion-based interpolation for seamless rotation. Both methods benefit from error minimization strategies and real-time adjustment algorithms to enhance precision in CNC machining and computer graphics applications.
Choosing the Right Interpolation Method
Choosing the right interpolation method depends on the geometry and application of your project. Linear interpolation moves toolpaths in straight lines, ideal for simple, direct movements, while circular interpolation follows arcs or curves, essential for round features and smooth transitions. Understanding the precise shape and complexity of your design ensures your machining process is efficient and accurate.
Linear Interpolation vs Circular Interpolation Infographic
 libmatt.com
libmatt.com