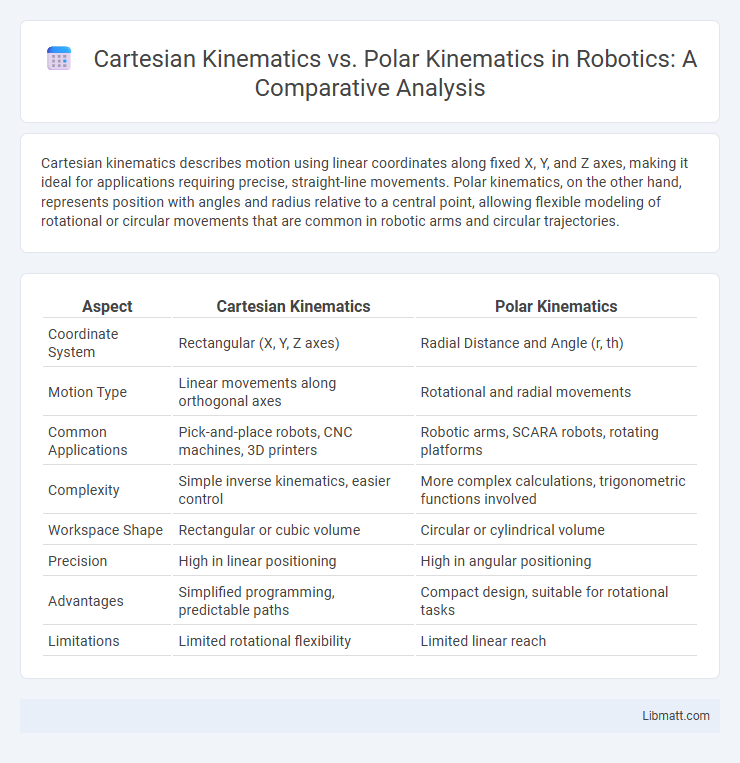
Cartesian kinematics describes motion using linear coordinates along fixed X, Y, and Z axes, making it ideal for applications requiring precise, straight-line movements. Polar kinematics, on the other hand, represents position with angles and radius relative to a central point, allowing flexible modeling of rotational or circular movements that are common in robotic arms and circular trajectories.
Table of Comparison
| Aspect | Cartesian Kinematics | Polar Kinematics |
|---|---|---|
| Coordinate System | Rectangular (X, Y, Z axes) | Radial Distance and Angle (r, th) |
| Motion Type | Linear movements along orthogonal axes | Rotational and radial movements |
| Common Applications | Pick-and-place robots, CNC machines, 3D printers | Robotic arms, SCARA robots, rotating platforms |
| Complexity | Simple inverse kinematics, easier control | More complex calculations, trigonometric functions involved |
| Workspace Shape | Rectangular or cubic volume | Circular or cylindrical volume |
| Precision | High in linear positioning | High in angular positioning |
| Advantages | Simplified programming, predictable paths | Compact design, suitable for rotational tasks |
| Limitations | Limited rotational flexibility | Limited linear reach |
Introduction to Kinematics
Kinematics studies motion without considering forces, focusing on the position, velocity, and acceleration of points or bodies. Cartesian kinematics utilizes a rectangular coordinate system to analyze motion along orthogonal x, y, and z axes, enabling straightforward calculations in linear movements. Polar kinematics employs radial and angular coordinates, best suited for rotational or circular motion, providing an efficient framework to describe trajectories around a fixed point.
Overview of Cartesian Kinematics
Cartesian kinematics describes motion using orthogonal x, y, and z coordinates, enabling precise position and velocity calculations in a rectilinear space. It simplifies the analysis of mechanisms and robotic arms by breaking down complex movements into independent linear components. This approach is ideal for systems operating in environments with defined linear constraints and enhances computational efficiency in trajectory planning.
Fundamentals of Polar Kinematics
Polar kinematics involves the study of motion using angles and radial distances relative to a fixed origin, making it ideal for systems with rotational or circular movements. Unlike Cartesian kinematics, which relies on x, y, and z coordinates, polar kinematics uses parameters like radius (r) and angle (th) to describe position and velocity, simplifying calculations in circular or oscillatory motions. Understanding the fundamentals of polar kinematics helps you analyze mechanisms such as robotic arms and rotating machinery with greater efficiency and precision.
Key Differences Between Cartesian and Polar Kinematics
Cartesian kinematics describes motion along straight, orthogonal x, y, and z axes, ideal for tasks requiring precise linear control and positioning. Polar kinematics, on the other hand, uses angles and radial distances to represent motion, which is advantageous for circular or rotational movements and simplifies calculations involving arc trajectories. Understanding these key differences allows you to select the appropriate kinematic model for optimizing robotic arm design and enhancing movement efficiency.
Mathematical Representation in Cartesian Coordinates
Cartesian kinematics uses a linear coordinate system with x, y, and z axes to describe the position, velocity, and acceleration of objects in space, expressed through vectors and matrices for straightforward computation. This representation simplifies the calculation of displacement and motion trajectories by breaking down movements into orthogonal components, making it particularly useful for robotic arm control and path planning. You can model complex motions with clear mathematical formulas involving partial derivatives and vector transformations in Cartesian coordinates, enhancing precision and predictability.
Mathematical Representation in Polar Coordinates
Polar kinematics uses angular displacement and radial distance to describe motion, with equations expressed in terms of radius (r) and angle (th), enabling precise modeling of rotational movements and curved trajectories. Unlike Cartesian kinematics, which relies on linear x and y coordinates, polar coordinates simplify the mathematics of circular or radial paths by directly relating position to angular velocity and radial velocity. Your understanding of polar kinematics enhances analysis of systems involving rotating arms, robotic joints, or any mechanism where motion pivots around a fixed point.
Advantages of Cartesian Kinematics
Cartesian kinematics offers precise and straightforward control of robotic movement in three-dimensional space using linear coordinates (X, Y, Z), facilitating easier programming and integration in industrial automation. Its linear nature simplifies inverse kinematics calculations, resulting in faster computation and improved accuracy for tasks such as pick-and-place operations. The Cartesian coordinate system also allows for scalable and modular robotic designs, enhancing flexibility and repeatability in manufacturing environments.
Benefits of Using Polar Kinematics
Polar kinematics offers significant advantages in applications involving rotational and angular motion due to its natural alignment with circular paths, simplifying calculations of joint angles and link positions. This system reduces computational complexity in robotic arms and mechanisms that pivot around fixed points, enhancing precision and control in tasks such as robotic surgery or antenna positioning. By directly correlating motion parameters with rotational coordinates, polar kinematics improves efficiency and accuracy over Cartesian kinematics in scenarios requiring radial and angular measurement.
Practical Applications and Examples
Cartesian kinematics excels in robotic arm control and CNC machine programming, where precise linear motion along X, Y, and Z axes is required. Polar kinematics is preferred in applications like radar systems, robotic arms with rotational joints, and radar tracking, utilizing radial distance and angular coordinates for efficient movement. Both kinematics systems are critical in fields such as automation, aerospace, and manufacturing for optimizing motion trajectories and achieving task-specific precision.
Choosing the Right Kinematic System
Selecting the right kinematic system depends on your robot's application and workspace requirements. Cartesian kinematics excels in linear, rectangular motion tasks such as CNC machining and 3D printing, providing straightforward coordinate control. Polar kinematics offers advantages in rotational and cylindrical tasks, delivering flexibility and range through angular movement around a fixed base.
Cartesian Kinematics vs Polar Kinematics Infographic
 libmatt.com
libmatt.com