Joint interpolation smoothly blends multiple data points or keyframes to create realistic animation or transitions, while linear interpolation calculates values along a straight line between two points, producing a more rigid, uniform progression. Understanding the difference helps you choose the best method for fluid motion or simple, predictable changes in your projects.
Table of Comparison
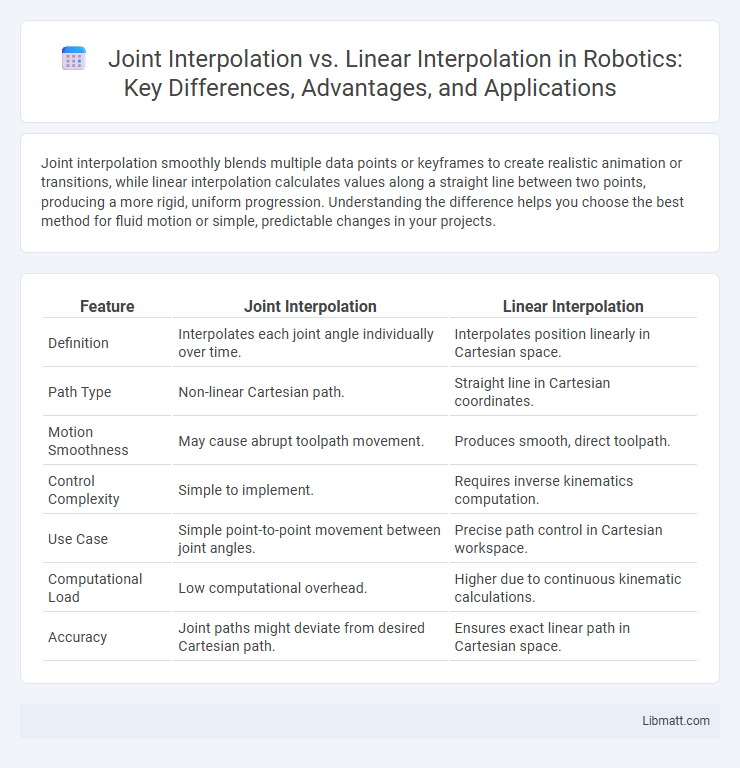
| Feature | Joint Interpolation | Linear Interpolation |
|---|---|---|
| Definition | Interpolates each joint angle individually over time. | Interpolates position linearly in Cartesian space. |
| Path Type | Non-linear Cartesian path. | Straight line in Cartesian coordinates. |
| Motion Smoothness | May cause abrupt toolpath movement. | Produces smooth, direct toolpath. |
| Control Complexity | Simple to implement. | Requires inverse kinematics computation. |
| Use Case | Simple point-to-point movement between joint angles. | Precise path control in Cartesian workspace. |
| Computational Load | Low computational overhead. | Higher due to continuous kinematic calculations. |
| Accuracy | Joint paths might deviate from desired Cartesian path. | Ensures exact linear path in Cartesian space. |
Introduction to Interpolation Methods
Joint interpolation combines multiple interpolation techniques to improve accuracy in multidimensional data estimation, making it suitable for complex datasets with varying patterns. Linear interpolation calculates intermediate values using straight-line segments between known data points, offering simplicity and efficiency in one-dimensional cases. Both methods serve essential roles in numerical analysis, with joint interpolation providing enhanced precision at the cost of increased computational complexity compared to linear interpolation.
What is Linear Interpolation?
Linear interpolation is a mathematical method used to estimate unknown values within two known data points by assuming a straight-line relationship between them. This technique calculates the value at a given position by proportionally scaling the difference between the known points, making it simple and efficient for one-dimensional data. It is widely used in fields like computer graphics, data analysis, and engineering for its straightforward implementation and speed.
What is Joint Interpolation?
Joint interpolation is a method used to estimate unknown values by considering multiple variables or dimensions simultaneously, often applied in multivariate data analysis and computer graphics. Unlike linear interpolation, which operates along a single axis or between two points, joint interpolation maps inputs across several parameters to produce a smooth, continuous approximation over complex data grids. It enhances accuracy in modeling relationships where data points depend on combined factors rather than isolated linear progression.
Key Differences Between Joint and Linear Interpolation
Joint interpolation combines multiple variables or data sets simultaneously, allowing for smooth transitions across multidimensional data points, whereas linear interpolation estimates values strictly along a straight line between two known points. The key difference lies in the complexity and application: joint interpolation handles interdependent variables for more accurate modeling in fields like robotics or animation, while linear interpolation is simpler and faster for one-dimensional data approximation. Understanding these distinctions helps optimize your choice of interpolation method based on data complexity and precision needs.
Mathematical Foundations of Each Method
Joint interpolation relies on multivariate polynomial functions to estimate values within a set of discrete points, capturing the dependencies among multiple variables simultaneously. Linear interpolation uses piecewise linear functions between two points, applying the formula \( y = y_0 + \frac{(y_1 - y_0)}{(x_1 - x_0)} (x - x_0) \), which assumes a constant rate of change between known data points. The mathematical foundation of joint interpolation supports higher-dimensional data estimation with potentially higher accuracy, while linear interpolation offers simplicity and computational efficiency for one-dimensional problems.
Applications in Animation and Robotics
Joint interpolation provides smooth rotation and natural motion in animation and robotics by directly interpolating joint angles, making it ideal for character rigging and robotic arm articulation. Linear interpolation, often used for straightforward position changes, is simpler but can result in unnatural, rigid movements when applied to rotational data. Advanced systems favor joint interpolation for precise control in complex, multi-joint motions, enhancing realism and functionality.
Pros and Cons of Linear Interpolation
Linear interpolation offers simplicity and computational efficiency, making it ideal for real-time applications and straightforward data sets. Its primary drawback is the creation of sharp edges or discontinuities, which can reduce accuracy in smooth curve approximations. This method lacks the flexibility to model complex or nonlinear data trends compared to joint or spline interpolation techniques.
Advantages and Limitations of Joint Interpolation
Joint interpolation offers the advantage of preserving smooth transitions across multiple data points, resulting in more accurate approximations for complex datasets compared to linear interpolation. It excels in capturing underlying trends by considering joint relationships, though it requires higher computational effort and can be sensitive to noise, leading to potential overfitting. Your choice of interpolation method should weigh the need for precision against these computational and stability considerations.
Choosing the Right Interpolation Method
Choosing the right interpolation method depends on the nature of your data and the desired outcome. Joint interpolation provides smoother transitions ideal for complex, non-linear datasets, while linear interpolation offers simplicity and faster computation for evenly spaced points. Your selection should balance accuracy with computational efficiency to best fit your specific application.
Conclusion: Which Method Suits Your Needs?
Joint interpolation excels in scenarios requiring smooth transitions across multiple dimensions, effectively handling complex datasets with interdependent variables. Linear interpolation offers simplicity and speed, making it ideal for straightforward, one-dimensional data with evenly spaced points. Choosing the right method depends on your data complexity, precision needs, and computational resources available.
Joint Interpolation vs Linear Interpolation Infographic
 libmatt.com
libmatt.com